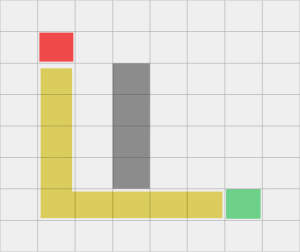Podstawy rekurencji, czyli o tym jak działa rekurencja. Wykorzystanie rekurencji w praktyce !

To już kolejny wpis poświęcony rekurencji w programowaniu, w którym wyjaśnię na praktycznym przykładzie, gdzie można ją wykorzystać. Rekurencja wcale nie musi być taka straszna, a jej użycie w praktyce może być łatwe i intuicyjne.

Źródło: flickr, Alexandre Duret-Lutz

Aktualnie tworzę grę komputerową, która będzie wykorzystywała elementy sztucznej inteligencji tj. znajdowanie ścieżki z wykorzystaniem algorytmu A*. Algorytm ten pozwala znaleźć optymalną ścieżkę z punktu A, do punktu B z uwzględnieniem wszystkich przeszkód po drodze, oraz biorąc pod uwagę ukształtowanie terenu (bagno, woda, las etc.).

Jeżeli mieliście do czynienia z algorytmem A* (A star), to wiecie, że podczas implementacji warto zwrócić uwagę na prawidłowy dobór przestrzeni poszukiwań. Wiele gier strategicznych korzysta z siatki prostokątów, rombów, lub kwadratów, które określają położenie danej jednostki.

Źródło: Źródło:

Załóżmy, że chcemy znaleźć ścieżkę z czerwonego pola, do pola oznaczonego kolorem zielonym. Pole oznaczone kolorem szarym to różnego rodzaju przeszkody na drodze, które należy ominąć. Naszą przestrzeń poszukiwań podzieliliśmy na siatkę prostokątów o jednakowych wymiarach. Teoretycznie nasza droga mogłaby wyglądać w ten sposób:

Źródło: Źródło:

Napisałem, że jest to droga teoretyczna, ponieważ w praktyce wszystko zależy od dodatkowych parametrów, które określimy w algorytmie np. czy uwzględnimy możliwość poruszania po ukosie itp. W najkrótszym wariancie będziemy musieli wykonać 10 ruchów, aby dostać się do zielonego pola.

Zanim algorytm odnajdzie optymalną ścieżkę z punktu A do punktu B to musi porównać ze sobą wiele pól – a im bardziej gęsta przestrzeń poszukiwań tym więcej porównań. Inaczej mówiąc, jeżeli nasze prostokąty będą zbyt małe, to czas znalezienia optymalnej ścieżki znacznie się wydłuży. W drugą stronę, jeżeli prostokąty będą zbyt duże to czas stworzenia przestrzeni poszukiwań może się znacznie wydłużyć, lub zakres ruchów będzie mocno ograniczony.

Jednym ze sposobów przyśpieszenia algorytmu A* jest zastosowanie prostokątów o różnych rozmiarach, które dopasowują się do terenu.

Źródło: Źródło: W praktyce wygląda to w ten sposób, że dzielimy przestrzeń poszukiwań na siatkę prostokątów o równych wymiarach, natomiast w momencie, gdy dany prostokąt obejmuje zasięgiem pole niedozwolone (np. przeszkodę) to dzieli się go na mniejsze prostokąty. Prostokąt dzielimy na 4 części do momentu, gdy dane pole będzie nadawało się do wykonania ruchu (nie będzie obejmowało zasięgiem pola niedozwolonego).

Na rysunku powyżej duże prostokąty (w środku) podzieliłem tylko 1 raz, na 4 mniejsze prostokąty. W praktyce (o czym pisałem powyżej) taki podział wykonuje się X-razy. Należy pamiętać, że w momencie gdy prostokąt obejmuje chociaż małą część pola niedozwolonego, to sam uznany jest jako pole niedozwolone, po którym nie można przejść. Widać to zwłaszcza na samym dole, gdzie ostatni niebieski prostokąt został wykluczony (nie jest brany pod uwagę podczas tworzenia ścieżki) – gdybyśmy dokonali jeszcze jednego podziału, to zyskalibyśmy większy zakres ruchów:

Źródło: Źródło: Nasza końcowa ścieżka odbywałaby się bliżej przeszkody (nie omijalibyśmy jej tak szerokim łukiem jak na poprzednim rysunku) – gdybyśmy dokonali jeszcze jednego podziału, to znów zyskalibyśmy większy i bardziej precyzyjny zasięg ruchu.

Przy zastosowaniu takiej przestrzeni poszukiwań ilość ruchów do wykonania w porównaniu z tym co mieliśmy na początku zmniejszyła się o połowę. Sukces !

Mam nadzieję, że wiecie co mam na myśli, a jeżeli nadal macie wątpliwości to zachęcam do zapoznania się z książką Perełki Programowania Gier, Vademecum Profesjonalisty. Tom 1. wyd. Helion, Mark DeLoura.

Co z tą rekurencją ?

Po tym dość długim wstępie wracamy do naszej rekurencji i jej praktycznego zastosowania w programowaniu. W przykładzie powyżej dzieliliśmy przestrzeń poszukiwań X-razy do momentu, gdy dane pole (prostokąt) umożliwiało swobodny ruch jednostki, lub gdy zachodził jeden z przyjętych przez nas warunków stopu (nie można dzielić przestrzeni poszukiwań bez końca !).

W praktyce realizacja tego zadania intuicyjnie powinna nas doprowadzić do zastosowania rekurencji. Najprostszy pseudokod funkcji, która odpowiadałaby za podział prostokątów na mniejsze części wyglądałby w ten sposób:

static public void Podziel(Prostokat pole) { 
if(pole zawiera pole_niedozwolone){
List obszar = PodzielProstokat();
    foreach(Prostokat obiekt in obszar) Podziel(obiekt);
}else {
 DopiszPoledoListyDozwolonej(pole);
 }
}

Na samym początku funkcji sprawdzamy, czy pole obejmuje zasięgiem obszar niedozwolony (pola wykluczone z ruchu np. przeszkody), jeżeli nie to mamy najprostszy przypadek, gdzie pole dopisywane jest do listy pól dozwolonych (takich, po których może być wytyczona ścieżka).

W przypadku, gdy pole obejmuje zasięgiem obszar niedozwolony (np. pokrywa się z przeszkodą), to musimy dokonać podziału takiego obszaru na 4 mniejsze podobszary i dla każdego z tych mniejszych podobszarów ponownie wykonać sprawdzenie.

W powyższym pseudokodzie nie uwzględniłem dodatkowych warunków, które byłyby konieczne do wykonania podziału tj. chociażby fakt, że nie trzeba dzielić obszaru, który w całości pokrywa pole niedozwolone – kolejne podziały w takim wypadku niczego nie zmienią (byłaby to pętla nie mająca końca).